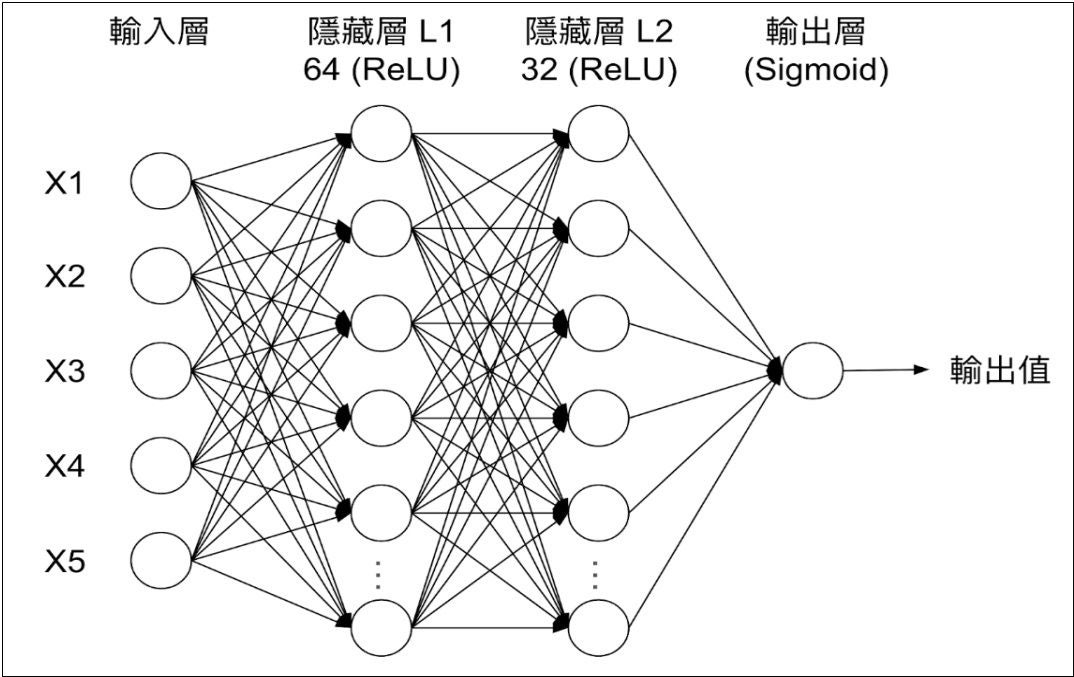
DNN 模型的學習過程包括前向傳播和反向傳播兩個階段:
- 前向傳播(Forward Propagation)階段:資料從輸入層開始逐層計算並傳遞至輸出層,如圖一中輸入了五個變數值,在每一層,神經元接收前一層的輸入,經過加權求和後,並通過激活函數(Activation Function)進行非線性轉換後輸出。
- 反向傳播(Back Propagation)階段:根據預測結果和真實值之間的誤差,使用反向傳播算法更新模型權重,這是一種基於梯度下降(Gradient Descent)的優化方法,通過計算誤差相對於每個權重的導數(梯度),來逐步調整權重,使模型計算的誤差逐步減小。
DNN模型的主要產出包括:
- 中間層輸出:資料經過每層神經元,搭配激活函數進行運算後,所取得在模型中經過每一層的處理結果。
- 預測機率:每筆資料透過模型逐層運算後,最終會得到對應該筆資料的預測機率,這個值介於0和1之間,亦可以解釋為該筆資料之預測結果為真的機率。
DNN模型的可解釋方法:SHAP方法的運作原理
DNN模型具有捕捉非線性關係的能力,並且在結合SHAP(Shapley Additive exPlanations) 方法後,更可以得到與Logistic Regression模型相似的可解釋性結果,為此,我們將在底下針對 SHAP 方法的運作原理進行說明。
SHAP方法是一種解釋機器學習模型的方法,用以量化每個特徵對模型產出結果的影響,從而提高 DNN 模型的透明度和可解釋性,讓使用者能更好地了解 DNN 模型並制定相關決策。透過將 SHAP 方法應用於 DNN 模型上,可以產出 SHAP 值來衡量每個特徵對預測結果的貢獻,SHAP 方法的核心思想是計算每個特徵在不同特徵組合中的貢獻,並取其平均值,這保證了分配的公平性和一致性。本文認為,透過將 DNN 模型結合 SHAP 方法,將可以幫助決策者更好地理解模型的預測過程和特徵重要性,從而做出更有依據的決策。
SHAP 方法在結合 DNN 模型後,提供以下優勢:
- 一致性:SHAP保證了特徵貢獻的分配與其實際重要性一致。對於金融機構而言,這意味著當某個自變數(例如利率上升)對預測結果的影響增大時,SHAP值會同步上升,這樣的特性能幫助使用者更準確地理解自變數變化對預測的影響,從而制定出更妥式的決策。
- 公平性:SHAP方法會藉由嘗試各個自變數存在或不存在的各種組合,並記錄各種組合下對模型原始產出結果的影響(舉例來說,嘗試當X1、X2及X4不存在時,模型預測值會減少0.5,並記錄下來),並用以計算出各個變數對於模型產出結果所造成的影響程度值,這種方式確保每個自變數的影響被公平地評估,避免只針對單一或少數自變數來評估變數的影響程度。在金融風險管理上,這能確保所有的自變數都得到合理考量,避免了單一或少數特徵主導預測結果的情況,提升評估的全面性與精確性。
- 全面與局部解釋:SHAP提供了全面特徵重要性分析,能幫助使用者了解哪些自變數對整體模型預測最為重要;同時,SHAP也能對單筆交易或特定客戶的預測結果進行詳細解釋,這讓金融機構能更深入地了解個別客戶行為,從而針對性地進行風險管理措施。實際上,除了風險管理的實務作業外,金融機構甚至更可以將此技術進一步擴展使用到日常的市場行銷作業中。
羅吉斯迴歸(Logistic Regression) 模型的運作原理
羅吉斯迴歸(Logistic Regression)是一種用於二元分類問題的統計模型,它通過自變數來預測一個二元的目標變數,模型假設自變數與目標變數之間的關係是線性的。
Logistic Regression模型的建構過程會使用訓練集的資料,通過最大概似估計(Maximum Likelihood Estimation)來求解模型參數,即各個自變數的係數。這些係數表示每個自變數對於預測目標變數的影響程度。模型建構完成後,便可透過模型計算每一筆測試資料對應的輸出值,並通過和 DNN 模型使用相同的 Sigmoid 函數,來將該值轉換為一個0到1之間的預測機率。
Logistic Regression 模型的主要產出包括:
- 係數:每個自變數的係數,這些係數反應了自變數對目標變數的影響大小。係數為正表示該自變數會使預測機率上升;反之係數為負則表示該自變數會使預測機率降低。
- 預測機率:每筆資料的預測機率,這個值介於0和1之間,可以解釋為該筆資料之預測結果為真的機率。
模型比較
針對DNN和Logistic Regression兩種模型,可透過下方表一了解兩者間不同的差異:
比較項目
| DNN
| Logistic Regression
|
資料處理能力
| 強:能夠處理雜訊(Noise)和複雜的資料型式。
| 弱:對資料的雜訊較敏感。
|
預測能力
| 優異:特別在處理高維度和非線性資料時表現出色,適合應用於金融市場的精細預測。
| 中等:對線性資料表現良好,但對非線性資料能力有限,適合基本分類任務,但在複雜問題上精度較低。
|
泛化能力
| 強:DNN 模型的泛化能力註1強,使其在面對新資料時仍能保持穩定的預測效果,以有效應對市場的多變性。
| 弱:泛化能力弱,當市場趨勢改變時,模型可能因為無法適應該變動而導致預測效果不佳。
|
模型解釋性
| 中等:模型複雜,但可以透過結合 SHAP 等工具,提供非線性任務上全面及局部的可解釋性結果,來輔助使用者進行重要決策。
| 高:模型簡單,可透過直接觀察係數來了解到各變數對模型結果的影響力,但效用僅限於線性任務,且只能夠提供全面的可解釋性。
|
適應性
| 高:能隨著資料和需求的變化進行靈活調整。
| 較低:難以應對資料的動態變化。
|
擴展能力
| 強:可通過增加層數和神經元數量來擴展模型的能力。
| 弱:擴展性有限,無法處理過於複雜的問題。
|
計算資源需求
| 高:在訓練過程中通常需要較多的計算資源及硬體設備(如GPU、TPU)支持。
| 低:資源需求較少,能快速計算。
|
訓練時間
| 長:多層結構及複雜運算使得訓練時間較長。
| 短:由於結構簡單,訓練速度較快。
|
部署成本
| 較高:初始成本較高,但能帶來更高的長期回報。
| 低:初始成本低,但長期效果有限。
|
註1:泛化能力(Gereralization):係指模型在處理與訓練資料來自相同分佈,但未曾學習過的新資料時,仍能夠進行正確預測的能力。換句話說,這種能力讓模型不僅在訓練資料上表現良好,在面對新資料時也能維持穩定的預測效果,證明模型所學到的規則能夠廣泛應用。
針對 DNN 和 Logistic Regression 兩種模型,可透過下方表一了解兩者間不同的差異:
比較項目
| DNN
| Logistic Regression
|
模型優勢總結
| DNN 模型因其具有高度的架構靈活性,能根據不同的金融議題靈活調整層數、神經元數量等結構,在處理金融業中高度複雜、非線性以及需要精準度高的金融預測議題上,表現相當出色。
| Logistic Regression 模型在需求相對簡單、線性、並且資料結構較為規則的情境中較有優勢,適合基本分類和預測需求,但在面對複雜資料時力有未逮。
|
適用情境
| 比如在信用行為分析中,DNN模型能有效分析客戶的大量行為數據,如交易紀錄、消費模式等,並結合市場波動、經濟數據來預測客戶行為。而在詐欺檢測方面,DNN 模型也可以從海量的交易資料中自動學習詐騙行為的隱藏模式,偵測到傳統模型無法察覺的異常行為。
此外,DNN 模型的高泛化能力使其在金融市場中表現突出,尤其在量化交易策略場景中,能捕捉非線性市場變動並提供精確的市場趨勢預測,從而協助投資決策;以及面對高頻交易的情境,DNN 模型也能有效預測市場的短期波動,提供交易機會。
| 比如處理基本風險分類的需求,如客戶的風險等級評估,模型能快速生成清晰且易於解釋的結果,以協助企業制定對應的風控策略;在信用卡申請審批或簡單的客戶分類任務中,模型能通過對基本的財務指標進行建模,快速給出結果,且因其具有可解釋性,決策者可以直接理解每個變數對風險預測的貢獻。
|
應注意事項
| 由於DNN模型的訓練和運行需要大量計算資源和較高的技術門檻,因此適合那些擁有充足資源、技術團隊完善的大型金融機構。這些機構通常需要應對瞬息萬變的市場變化,因此DNN模型的強大預測能力和靈活性將能為其帶來長期增值效益。
| Logistic Regression模型的優勢在於可以快速訓練、部署成本低,適合穩定的業務需求或資料變動較少的情境,如常規貸款風險管理,但在面對高複雜度、非線性資料時,其預測能力仍不比DNN模型準確。
|
總結來說,通過說明模型方法論並比較不同模型間的差異,可以發現DNN模型在多方面顯示出優於Logistic Regression模型的效果:
- 更高的預測能力:DNN模型能夠透過反覆訓練提取模型特徵,從而識別和預測客戶行為;與Logistic Regression單向模型建製流程相比,DNN 模型的前向傳播和反向傳播兩個階段使其對於模型資料擁有更高的掌握度,亦可提供優於Logistic Regression模型的預測能力。舉例來說,對於資料更新頻率較低的變數,可提供更敏感且準確的預測效果。
- 更深入的解釋能力:DNN模型配合SHAP方法,可以清楚地了解各自變數對模型預測結果的影響,亦能夠針對單筆資料分析各自變數對模型結果的具體貢獻。
這些結果強調了DNN模型在處理複雜非線性關係上的優勢。惟金融機構若為導入DNN模型,將可能面臨以下潛在挑戰:
- 模型訓練所需時間較長,資源需求較高:由於DNN模型的多層結構和大量參數,訓練過程中需要進行大量的矩陣運算,這需要強大的計算資源(如GPU),且訓練DNN模型通常需要大量的訓練迭代和調參過程,這會耗費較長的時間。
- 為確保可解釋性,模型需額外搭配其他方法(如SHAP方法):由於 DNN 模型的複雜性,其內部運作過程對於需要透過不同方法提取模型特徵/自變數的金融機構而言,可能是個挑戰。